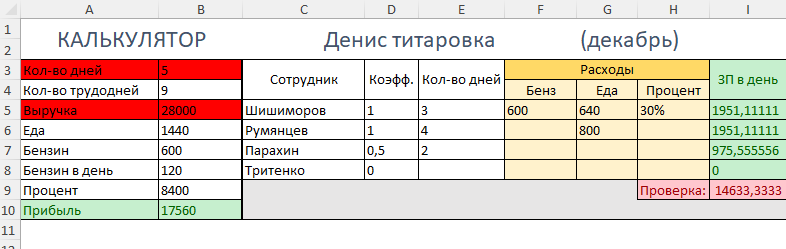
Для решения задачи недостаточно данных о коэффициентах мастеров. Для точного расчёта нужно узнать коэффициенты Шишиморова и Румянцева, а также базовую ставку оплаты (допустим, что та же ставка была бы у Парахина, если бы он не был стажером и получал полную оплату).
Допустим, что базовая ставка оплаты в день для мастера без коэффициента равна \( X \). Тогда:
- Парахин получает \( 0,5X \) в день, так как он стажер.
- Шишиморов получает \( X \cdot K_{Ш} \) в день, где \( K_{Ш} \) — его коэффициент.
- Румянцев получает \( X \cdot K_{Р} \) в день, где \( K_{Р} \) — его коэффициент.
Суммарная прибыль за все дни труда трёх мастеров равна:
\[ \text{Общая прибыль} = Шишиморов_{дни} \cdot (X \cdot K_{Ш}) + Румянцев_{дни} \cdot (X \cdot K_{Р}) + Парахин_{дни} \cdot (0,5X) \]
\[ 17560 = 3 \cdot X \cdot K_{Ш} + 4 \cdot X \cdot K_{Р} + 2 \cdot 0,5X \]
Раскроем скобки и упростим выражение:
\[ 17560 = 3XK_{Ш} + 4XK_{Р} + X \]
Однако, без значений \( K_{Ш} \) и \( K_{Р} \), мы не можем вычислить значение \( X \) и, следовательно, точную зарплату в день для каждого мастера.
Если бы у нас были эти значения, мы могли бы решить уравнение относительно \( X \), а затем вычислить зарплату в день для каждого мастера, как показано выше. Пожалуйста, предоставьте необходимую информацию для точного расчёта.