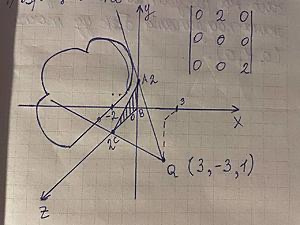
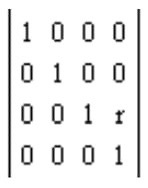
Проецирующая матрица используется для преобразования точек из одного пространства в другое, например, из трёхмерного пространства в двумерное, что и является сутью проецирования тени на экран. Это преобразование может быть выполнено с помощью линейной алгебры и матричных операций.
Для определения координат тени с использованием проецирующей матрицы, необходимо воспользоваться следующим алгоритмом:
1. Определить вектор направления от источника света к точке объекта (Q - P).
2. Найти точку пересечения данного вектора с плоскостью (назовём её S), где будет находиться "тень" точки.
3. Использовать проецирующую матрицу для преобразования координат точки S в координаты на экране.
Формулы для вычисления будут зависеть от определенных параметров: источника света, плоскости и системы координат, в которой определены все эти элементы. Для трёхмерного пространства в общем случае работа будет выглядеть так:
Например, плоскость определяется уравнением Ax + By + Cz + D = 0, где (A, B, C) - вектор нормали плоскости, а D - расстояние от начала координат до плоскости по вектору нормали.
Если у нас есть точка на объекте P с координатами (Px, Py, Pz) и точка-источник света Q с координатами (Qx, Qy, Qz), вектор направления от источника света к точке P будет иметь координаты (Px-Qx, Py-Qy, Pz-Qz).
Для нахождения точки пересечения S можно решить систему уравнений, сочетая параметрическое представление прямой с уравнением плоскости:
S = Q + t(P - Q)
где t - параметр, который нам нужно найти. Подставляя S в уравнение плоскости, мы можем решить его для t, а затем находим координаты точки S.
После того, как мы нашли координаты S в трёхмерном пространстве, мы можем преобразовать их в координаты экрана, используя проецирующую матрицу M:
S_screen = M * S
Координаты S_screen будут содержать координаты тени на экране, где M - это матрица, преобразующая координаты из одного пространства в другое.
Так как процесс проецирования обычно включает в себя переход от трёхмерного пространства к двумерному, чаще всего после умножения на матрицу мы получаем четырёхмерные векторы (из пространства с однородными координатами). Координаты точки на экране мы можем получить, выполнив перспективное деление, то есть разделив x и y на w:
x_screen = S_screen.x / S_screen.w
y_screen = S_screen.y / S_screen.w
Эти x_screen и y_screen будут координатами тени на экране.
В реальных компьютерных графиках и игровых движках весь процесс может быть более сложным и включать использование нескольких матриц преобразов