Чтобы найти координаты тени, которая падает на какую-либо плоскость, необходимо выполнить несколько шагов, используя линейную алгебру и основы компьютерной графики. Последовательность действий:
1. **Определение вектора света:**
Из координат источника света `L` (x_l, y_l, z_l) и координат точки объекта `P` (x_p, y_p, z_p), вычислите направляющий вектор света `V` путем вычитания координат точки из координат источника света: `V = L - P`.
2. **Параметрическое уравнение линии:**
Запишите параметрическое уравнение линии, идущей от точки `P` в направлении вектора `V`: `P(t) = P + tV`, где `t` — параметр, `"+"` обозначает векторное сложение, а `tV` — скалярное умножение вектора `V` на `t`.
3. **Уравнение плоскости:**
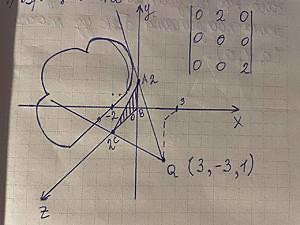
Определите уравнение плоскости `Ax + By + Cz + D = 0`, на которую падает тень, используя координаты нормали плоскости `N` (A, B, C) и одну из точек на плоскости (если заданы точки, вы можете вычислить нормаль как векторное произведение двух векторов, лежащих в плоскости).
4. **Нахождение точки пересечения:**
Подставьте параметрическое уравнение линии в уравнение плоскости и решите его относительно `t`. Плоскость и линия пересекутся, когда `Ax_p(t) + By_p(t) + Cz_p(t) + D = 0`. Решение этого уравнения даст вам значение параметра `t` в точке пересечения.
5. **Вычисление координат тени:**
Подставьте найденное значение `t` обратно в параметрическое уравнение линии, чтобы найти координаты точки пересечения на плоскости, что и будет координатами тени объекта.
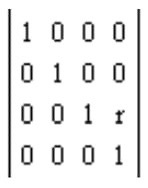
Обратите внимание, что проецирующая матрица обычно используется в компьютерной графике для проецирования трехмерных координат в двумерное пространство экрана и не применяется напрямую для вычисления координат тени на объектах в трехмерном пространстве. Чтобы вычислить тень на основе проецирующей матрицы, необходимо сперва использовать матрицу перехода от координат источника света к координатам на плоскости.
Если координаты источника света и плоскость, на которую падает тень, заданы в системе координат, отличной от системы координат экрана, вас может заинтересовать преобразование координат тени в экранное пространство. Для этого вам потребуется композиция матриц трансформации, которая может включать модельную матрицу (для преобразования в мировые координаты), вида (для преобразования в координаты камеры) и проекционной матрицы (для проецирования в координаты эк