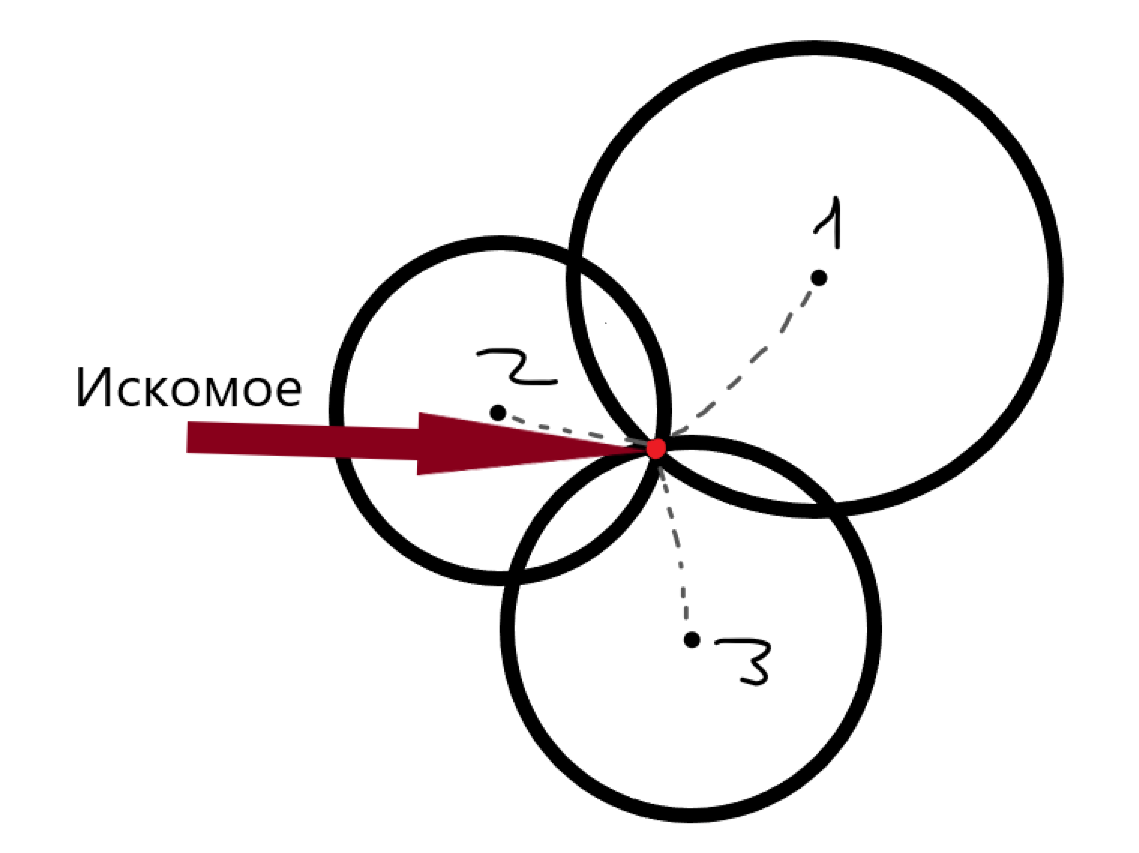
Как найти координаты точки пересечения трех окружностей, если известны их центры и радиусы?
Как можно найти координаты точки пересечения трех окружностей, имея информацию о координатах их центров и расстояниях от центров до точки пересечения? Если привести это к абстрактному случаю, нам даны координаты трех точек на плоскости и их расстояния до некоторой другой точки. Как можно использовать Python, включая библиотеку sympy, чтобы найти координаты этой другой точки?
- 14 декабря 2023 г. 16:17
Для нахождения координат точки пересечения трех окружностей можно воспользоваться библиотекой sympy. Вот пример кода на языке Python:
```python
from sympy import Point, Circle
# Задаем центры окружностей и радиусы
center1 = Point(x1, y1)
radius1 = r1
center2 = Point(x2, y2)
radius2 = r2
center3 = Point(x3, y3)
radius3 = r3
# Создаем объекты окружностей
circle1 = Circle(center1, radius1)
circle2 = Circle(center2, radius2)
circle3 = Circle(center3, radius3)
# Находим точки пересечения окружностей
intersection_points = circle1.intersection(circle2, circle3)
# Выводим координаты точек пересечения
for point in intersection_points:
print("x =", point.x, "y =", point.y)
```
В коде выше мы задаем координаты центров окружностей и их радиусы. Затем создаем объекты окружностей с помощью класса `Circle` из библиотеки sympy. Используя метод `intersection`, мы находим точки пересечения окружностей. Результатом будет список объектов `Point`, из которых можно получить координаты точек пересечения с помощью атрибутов `x` и `y`.
Сначала решить систему уравнений чтобы найти точки пересечения двух окружностей. Примем xi, yi за центр, а Ri за радиус. Тогда получим:
(x - xA)^2 + (y - yA)^2 = RA^2
(x - xB)^2 + (y - yB)^2 = RB^2
Раскрываем скобки, вычитаем первое уравнение из второго, получаем квадратное уравнение. 2 корня - 2 точки пересечения, 1 корень - одна точка касания, нет корней - окружности не пересекаются.
Потом эти точки (1 или 2) проверить на принадлежность третьей окружности, т.е. убедиться что выполняется условие (x - xС)^2 + (y - yС)^2 = RС^2. Проверку выполнения нужно проводить с некоторой точностью, т.е. сравнение делать не a == b, а скорее в духе abs(a - b) < 0.000001.
Вот и всё.
Если можно использовать sympy, то можешь попробовать сразу задать систему из трёх уравнений в нём.