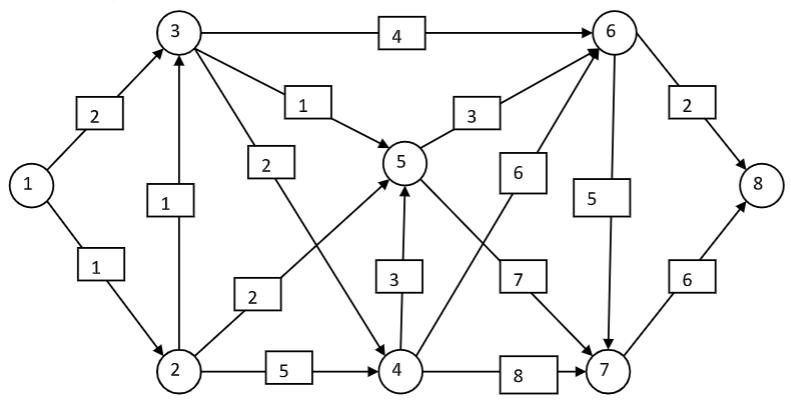
Алгоритм Дейкстры традиционно применяется к графам, представленным в виде матрицы смежности, где каждый элемент `A[i][j]` представляет вес ребра от вершины `i` к вершине `j`. Однако матрица инцидентности представляет граф в другом виде: здесь строки соответствуют вершинам, а столбцы — ребрам. Элемент матрицы инцидентности `M[v][e]` равен:
- `-1`, если ребро `e` исходит из вершины `v` (для ориентированного графа),
- `1`, если ребро `e` входит в вершину `v` (для ориентированного графа),
- Вес ребра, если ребро `e` инцидентно вершине `v` (для взвешенного графа),
- `0`, если вершина `v` не инцидентна ребру `e`.
Для применения алгоритма Дейкстры к графу, представленному таким образом, вам необходимо преобразовать матрицу инцидентности в что-то, что позволяет легче найти соседей каждой вершины и веса рёбер. Например, можно использовать список смежности, где для каждой вершины вы будете хранить веса рёбер до всех соседей.
Этапы преобразования матрицы инцидентности в список смежности могут выглядеть примерно так:
1. Пройдите по столбцам матрицы инцидентности. Для каждого столбца определите две вершины `v1` и `v2` и вес ребра `w` между ними.
2. Добавьте информацию о смежности и весе ребра в список смежности. Например, если ребро ведёт из `v1` в `v2` с весом `w`, добавьте `v2` с весом `w` в список смежности для `v1`.
Пример преобразования на псевдокоде:
```
function convertToAdjacencyList(incidentMatrix):
adjacencyList = new List<List<Pair<int, int>>>() // Создаем список смежности
for каждый столбец col в incidentMatrix:
v1 = null
v2 = null
w = null
for каждая строка row в col:
if incidentMatrix[row][col] < 0:
v1 = row
else if incidentMatrix[row][col] > 0:
v2 = row
w = incidentMatrix[row][col]
if v1 != null и v2 != null и w != null:
adjacencyList[v1].add(new Pair(v2, w)) // Добавляем смежность и вес
return adjacencyList
```
После преобразования матрицы инцидентности в список смежности вы можете использовать стандартный алгоритм Дейкстры, который работает непосредственно с данным списком.
Напоминаем, что алгоритм Дейкстры ищет кратчайшие пути от заданной начальной вершины до всех остальных вершин в графе и не может быть использован в графах с отрицательными весами рёбер. Если ваш граф может содержать отрицательные веса, рассмотрите использование алгоритма Беллмана-Форда.