Как определить координаты точек, где два многоугольника пересекаются?

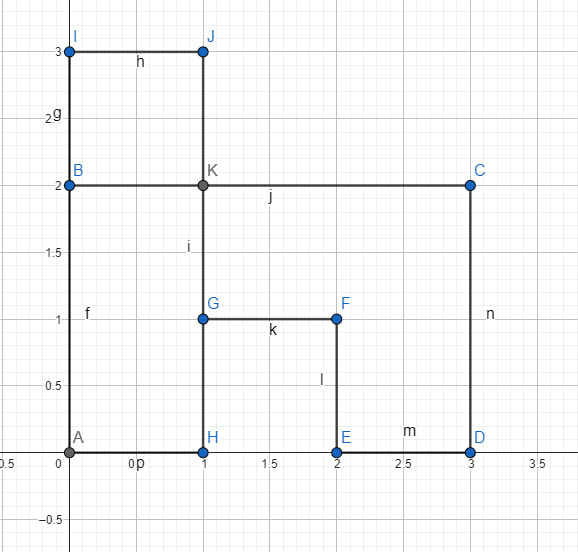
Для определения координат точек, где два многоугольника пересекаются, можно использовать алгоритм пересечения полигонов. Ниже приведен пример такого алгоритма:

1. Начните с выбора одного из многоугольников, назовем его "Многоугольник A". Пройдите по всем его вершинам.

2. Для каждой вершины Многоугольника A проверьте, пересекается ли линия, образованная этой вершиной и следующей вершиной Многоугольника A (назовем их "Точка A" и "Точка B" соответственно), с каждой стороной другого многоугольника (назовем его "Многоугольник B"). Для этого можно использовать алгоритм проверки пересечения двух отрезков.

3. Если линия, образованная точками A и B, пересекается с какой-либо стороной Многоугольника B, найдена точка пересечения. Запишите ее координаты.

4. Повторите шаги 2-3 для каждой вершины Многоугольника A.

5. Если точки пересечения найдены, верните их координаты. Если точек пересечения нет, то многоугольники не пересекаются.

Если стороны полигональных областей пересекаются по отрезку, то можно использовать алгоритм пересечения отрезков. Ниже приведен пример такого алгоритма:

1. Проверьте, пересекаются ли отрезки двух полигонов. Для этого можно использовать алгоритм проверки пересечения двух отрезков.

2. Если стороны полигональных областей пересекаются, найдена точка пересечения. Запишите ее координаты.

3. Повторите шаги 1-2 для каждой пары сторон двух полигонов.

4. Если точки пересечения найдены, верните их координаты. Если точек пересечения нет, то полигоны не пересекаются.

Обычно я определяю прямоугольник таким образом: его левая и верхняя сторона включаются в него, а правая и нижняя сторона считаются за пределами. На математическом языке запись будет выглядеть так: (x1 ≥ x > x2, y1 ≥ y > y2). Это позволяет строить прямоугольники плотно рядом, не пересекаясь, в любых координатах, будь то целые числа, числа с плавающей запятой и так далее.