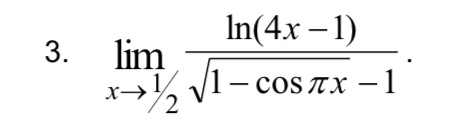Если в задаче присутствует функция, у которой предел приближается к определенной форме, то кроме применения правила Лопиталя есть и другие методы решения.
1. Метод разложения в ряд Тейлора. Иногда можно разложить заданную функцию в ряд Тейлора вокруг определенной точки и использовать несколько начальных членов ряда для анализа предела.
2. Применение алгебраических преобразований. В некоторых случаях можно преобразовать задачу алгебраическими преобразованиями, такими как умножение на сопряженное выражение или факторизация выражений.
3. Подстановка переменных. Замена переменных может привести к упрощению задачи и упрощению выражения для вычисления предела.
4. Использование известных тождеств и свойств функций. Зачастую известные тождества и свойства функций позволяют упростить выражения и помочь в анализе пределов.
В каждой конкретной задаче нахождения предела без использования правила Лопиталя может потребоваться комбинация этих методов или какой-то специфический подход, так как каждая задача индивидуальна.