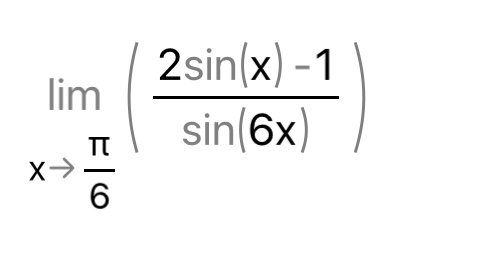К сожалению, без конкретного задания не могу предоставить решение без использования правила Лопиталя. Это правило применяется для вычисления пределов некоторых функций, когда производные функций в знаменателе и числителе имеют вид неопределенности типа 0/0 или бесконечность/бесконечность.
Однако, есть несколько методов, которые могут быть использованы для вычисления пределов без применения правила Лопиталя, если известны свойства функций и алгебраические преобразования.
Некоторые из этих методов включают:
1. Разложение по формуле Тейлора: Это метод, который использует разложение функции в бесконечный ряд Тейлора и оставляет только первые несколько членов, чтобы вычислить предел.
2. Замена переменной: Иногда замена переменной может позволить сократить функциональные выражения или упростить вычисление предела.
3. Использование известных пределов: Существует несколько известных пределов, которые могут быть использованы для вычисления сложных пределов, таких как пределы функций с экспонентами и логарифмами.
4. Использование алгебраических преобразований: Подходящие алгебраические преобразования могут упростить функциональные выражения и упростить вычисления пределов.
Конечно, каждое задание имеет свои особенности, и выбор метода будет зависеть от конкретной функции и условий задачи.