Как вычислить определитель с использованием многоточия?

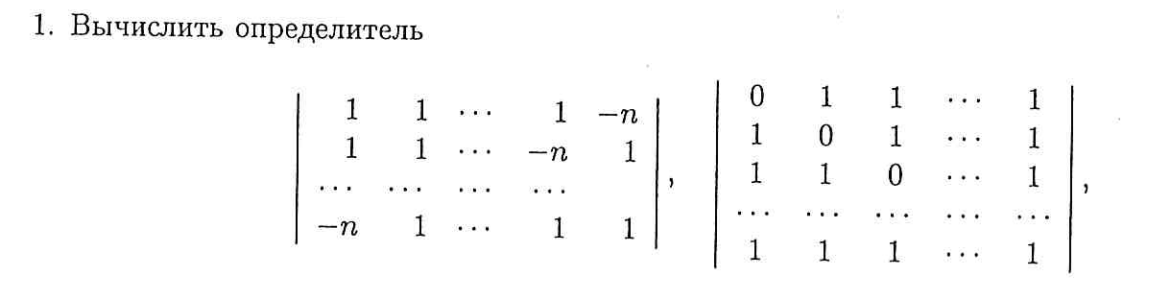
Одним из способов вычисления определителя с использованием многоточия является применение метода Гаусса-Жордана. Этот метод позволяет привести матрицу к ступенчатому виду и дальше получить определитель, перемножив диагональные элементы.

Пример:

Рассмотрим матрицу 3x3:
A = |1 2 3|
       |4 5 6|
       |7 8 9|

Применим метод Гаусса-Жордана для приведения матрицы к ступенчатому виду:

1) Первая строка остается неизменной.
2) Вычитаем из второй строки первую, умноженную на 4:
   |1  2  3|
   |0 -3 -6|
   |7  8  9|
   
3) Вычитаем из третьей строки первую, умноженную на 7:
   |1  2  3|
   |0 -3 -6|
   |0 -6 -12|
   
4) Делим вторую строку на -3:
   |1 2 3|
   |0 1 2|
   |0 -6 -12|
   
5) Вычитаем из третьей строки вторую, умноженную на -6:
   |1 2 3|
   |0 1 2|
   |0 0 0|
   
Матрица приведена к ступенчатому виду. Определитель равен произведению элементов на главной диагонали: 1 * 1 * 0 = 0.

Схожий пример:

Рассмотрим матрицу 4x4:
A = |2 0 1 3|
       |3 1 0 2|
       |1 3 2 0|
       |0 2 3 1|

Применим метод Гаусса-Жордана и приведем матрицу к ступенчатому виду:

1) Первая строка остается неизменной.
2) Вычитаем из второй строки первую, умноженную на 3/2:
   |2  0   1   3|
   |0  1  -3/2 -1/2|
   |1  3   2   0|
   |0  2   3   1|
   
3) Вычитаем из третьей строки первую, умноженную на 1/2:
   |2  0   1   3|
   |0  1  -3/2 -1/2|
   |0  3/2 3/2 -3/2|
   |0  2   3   1|
   
4) Вычитаем из четвертой строки первую, умноженную на 0:
   |2  0   1   3|
   |0  1  -3/2 -1/2|
   |0  3/2 3/2 -3/2|
   |0  2   3   1|
   
5) Вычитаем из четвертой строки вторую, умноженную на 2:
   |2  0   1   3|
   |0  1  -3/2 -1/2|
   |0  3/2 3/2 -3/2|
   |0  0   6   2|

Матрица приведена к ступенчатому виду. Определитель равен произведению элементов на главной диагонали: 2 * 1 * (3/2) * 6 = 18.

Таким образом, определитель матрицы A равен 18.

Многоточие используется для замены подобных символов или цифр.
Например, под первой матрицей может скрываться следующая последовательность: и1 -n, -n 1 и1 1 1 -n, 1 1 -n 1, 1 -n 1 1, -n 1 1 1, где символ "-n" заменяет однотипные элементы и "и1" обозначает наличие единиц на диагонали и единицы в остальных местах. Определение каждой матрицы зависит от ее размера и содержания.

П.С. Второй пример не является наилучшим, так как требуется догадываться о наличии нулей на диагонали.