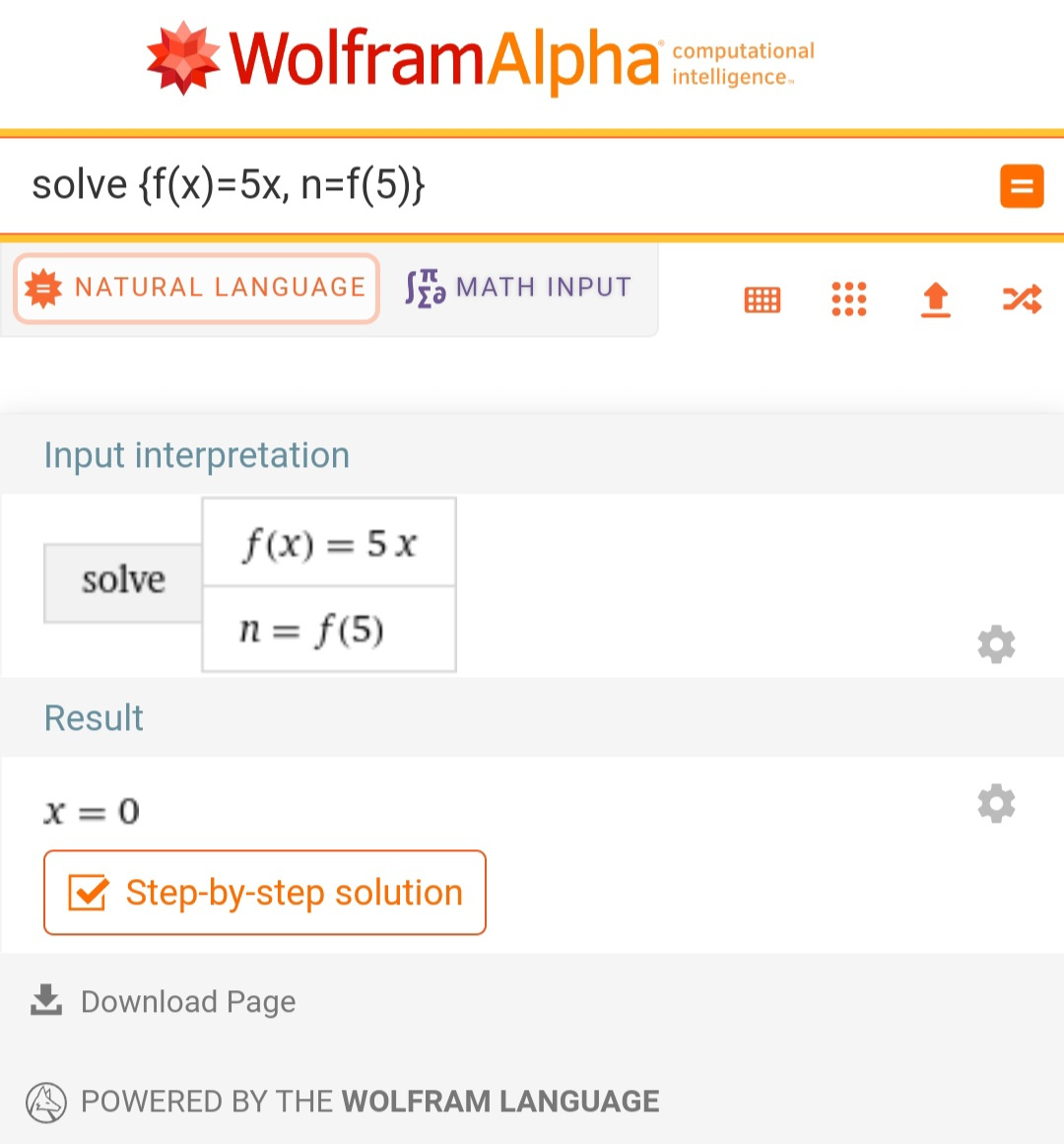
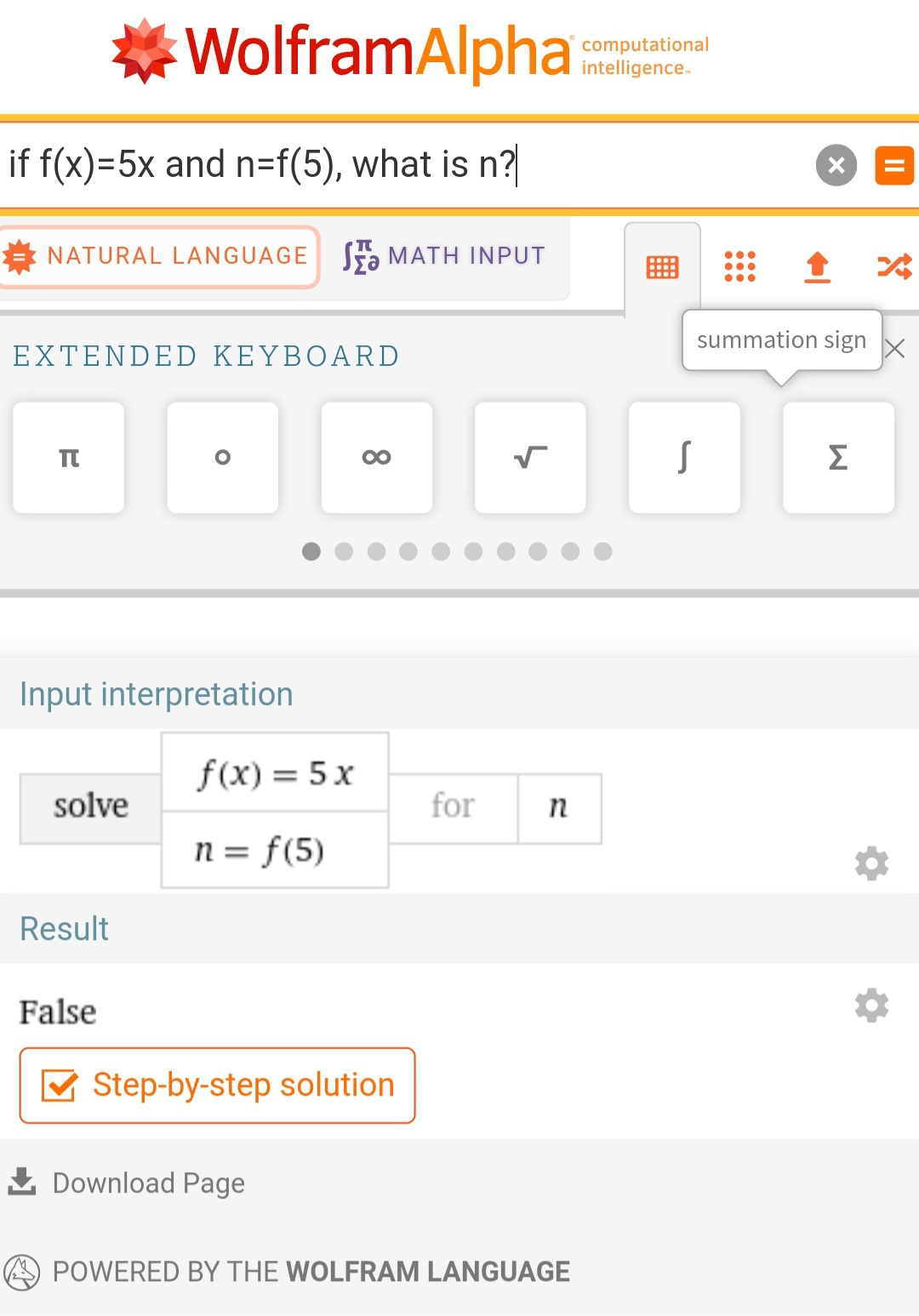
Чтобы создать систему уравнений с использованием функций в Wolfram Alpha, вы можете использовать стандартный синтаксис для записи уравнений. Вот пример:
```
Solve[{x^2 + y^2 == 25, x + y == 7}, {x, y}]
```
Этот пример решает систему уравнений, состоящую из уравнений x^2 + y^2 == 25 и x + y == 7, и находит значения переменных x и y.
Однако, если одно из уравнений содержит функции, решение может быть более сложным. В этом случае вам может потребоваться использовать определенные команды и подходы для получения желаемого результата.
Если вы хотите найти область возможных значений для переменной n в системе уравнений с функциями, можно попробовать использовать команду `Reduce`. Вот пример:
```
Reduce[{Sin[x] + Cos[y] == n, x + y == 3}, n]
```
В этом примере мы хотим найти область значений переменной n, при которых выполняются уравнения Sin[x] + Cos[y] == n и x + y == 3.
Однако не всегда возможно найти аналитическое решение, особенно если функции сложные или система уравнений нелинейна. В таких случаях вы можете использовать численные методы или символьные вычисления, чтобы приблизительно найти решение.
Надеюсь, эти рекомендации помогут вам решить вашу проблему в Wolfram Alpha. Если у вас возникнут ещё вопросы, не стесняйтесь задать.