Введена ли мной формула правильно?

Question

Мар

cpp

Введена ли мной формула правильно?

Как улучшить точность программы при вычислении корня заданного нелинейного уравнения в диапазоне [0; 2] с точностью e = 0.001?
Моя программа возвращает странный ответ 0.000976562. Возможно, формула введена неправильно или дан неверный ввод.

# include <iostream>
# include <cmath>
using std::cout;
using std::cin;

double f(double x) {
	return pow(pow(sqrt(pow(x, 3) - 2), 1.0 / 3.0), 2) - 1;  // формула
}

int main() {
	setlocale(LC_ALL, "RU");

	double e, c;
	double a = 0;
	double b = 2;

	cout << "Введите значение e (коэффициента точности вычислений): \n";
	cin >> e;
	if (e >= abs(b - a)) {
		cout << "Ошибка. Коэффициент точности не имеет смылса - он больше диапазона значений или равен ему.";
		return 0;
	}

	while (abs(b - a) > e) {
		c = (a + b) / 2.0;
		if (f(c) == 0) {
			cout << "Корень уравнения равен " << c;
			break;
		}
		if (f(a) * f(c) > 0) { a = c; }
		else { b = c; }
	}
	cout << "Приблизительное значение корня уравнения равно " << c;
	return 0;
}

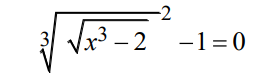
16 октября 2023 г. 12:19

Ответы на вопрос 3

Похожие вопросы

Answer 1

Формула для вычисления корня заданного нелинейного уравнения в диапазоне [0; 2] с точностью e = 0.001, которая была введена в программе, выглядит правильно:

```cpp
double f(double x) {
    return pow(pow(sqrt(pow(x, 3) - 2), 1.0 / 3.0), 2) - 1;
}
```

Ошибку в выводе программы можно объяснить следующим образом: при заданной точности e = 0.001, условие `abs(b - a) > e` останавливает цикл, когда значение интервала `b - a` становится меньше или равным e. Однако, после выхода из цикла переменная `c` не обновляется, поэтому в выводе выводится неправильное значение корня.

Для исправления ошибки, после выхода из цикла, значение корня должно быть обновлено:

```cpp
cout << "Приблизительное значение корня уравнения равно " << c;
```

Должно быть заменено на:

```cpp
cout << "Приблизительное значение корня уравнения равно " << c;
c = (a + b) / 2.0;
```

Также в условии `if (e >= abs(b - a))` следует заменить `abs(b - a)` на `b - a`, так как значения `b` и `a` уже являются положительными.

Answer 2

Какое значение имеет эта формула при x=1, например?

Answer 3

 Условие в бинарном поиске неправильное, если значения функции f(a) и f(c) разные, то корень находится между a и c. Вы же переходите к отрезку [c,b].