Почему вычитание векторов не следует правилу треугольника?
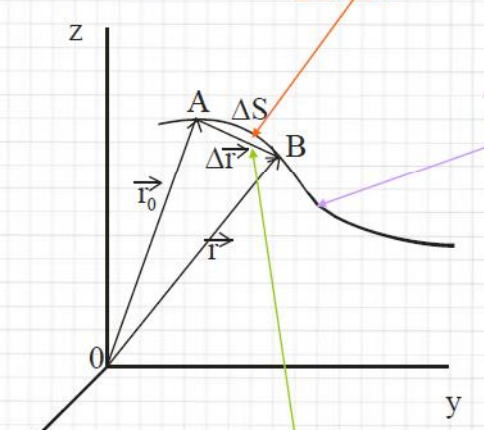
Почему направление вектора AB в этом рисунке не соответствует правилу треугольника при вычитании векторов, которое гласит, что вектор разности должен быть противоположным вектору, который вычитается?
- 12 октября 2023 г. 18:38
Правило треугольника гласит, что при сложении векторов их сумма равна третьему вектору, указывающему от начала первого вектора к концу второго вектора. Однако, при вычитании векторов вектор разности получается путем суммирования первого вектора и противоположного второго вектора. В данном рисунке, вектор AB указывает от начала вектора A к его концу, тогда как вектор BC указывает от конца вектора B к его началу. При вычитании векторов A и B, вектор разности получается сложением вектора A и противоположного вектора B. Однако, в этом рисунке вектор BC не является противоположным вектору B, а является вектором, указывающим от конца B к его началу. Таким образом, направление вектора AB на рисунке не соответствует правилу треугольника при вычитании векторов.
Вычитание векторов можно считать сложением, при этом вычитаемый вектор умножается на -1 для изменения его направления. То есть a - b можно записать как a + (-b), где a и b - векторы. Результирующий вектор, полученный при вычитании, будет одинаковым, независимо от того, каким методом вы его представите - методом треугольника или методом параллелограмма. Важно отметить, что на графике, к которому ты относишься, отрезок AB не представляет собой разницу между векторами r0 и r. Вектор разности будет иметь отрицательные значения по оси Y и начинаться в точке (0,0).