В какой части процесса могла возникнуть ошибка?
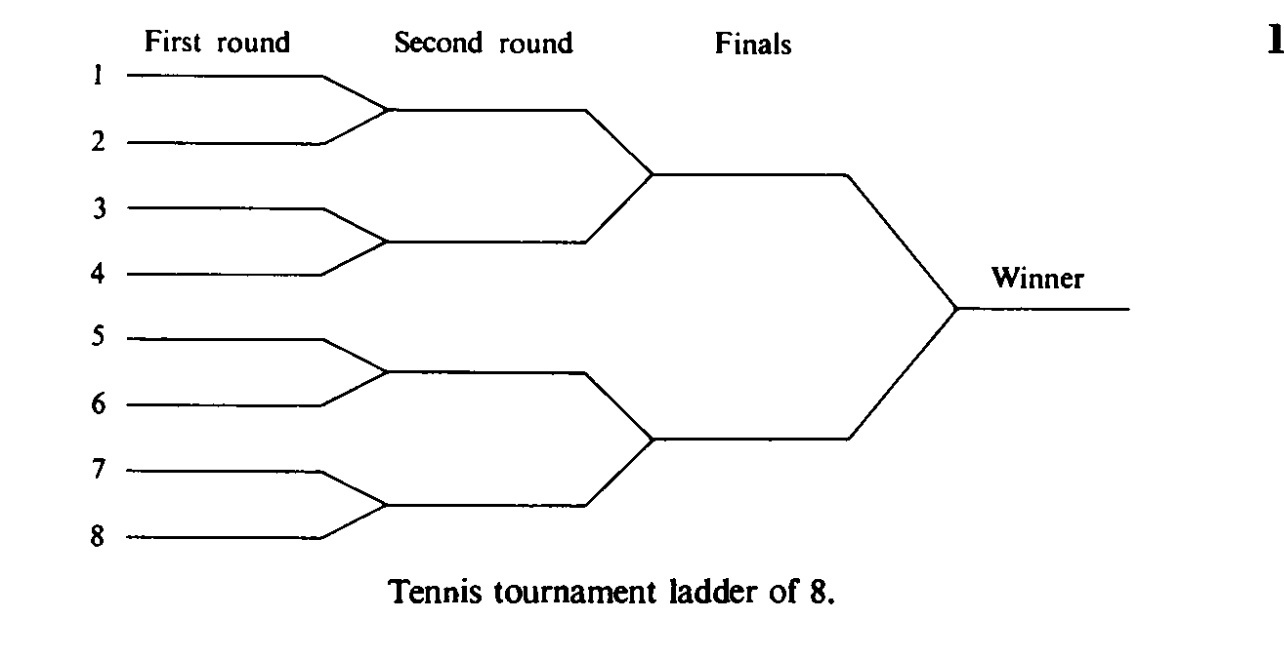
Вопрос: Как правильно рассчитать вероятность встречи двух игроков A и B на одной из игр в турнирной сетке на 8 человек? Решение автора: Я посчитал вероятность встречи игроков A и B на разных этапах турнира, но ошибка возникла в вычислении вероятности встречи на втором круге. Я не учел, что игрок B не может занимать позицию 2, если игрок A занимает позицию 1. Правильная вероятность на втором круге должна быть 2/6 * 1/4. В итоге, правильный ответ равен 1/7 * 1 + 2/6 * 1/4 + 4/7 * 1/16 = 0.25744047619. Моя попытка решения: Я посчитал вероятность встречи игроков A и B на разных этапах турнира и использовал комбинаторику. При этом получил такой же результат - вероятность встречи равна 0.25. Что я упустил в своих рассуждениях?
- 8 октября 2023 г. 19:47
Вы упустили то, что вероятность встречи игроков A и B на втором круге зависит от того, встретились ли они на первом круге. Если игроки встретились на первом круге, то вероятность встречи на втором круге будет 0, так как они уже встретились и по определению турнирной сетки не могут встретиться вновь. Эту ситуацию вы не учли в своих рассуждениях, поэтому получили несовпадающий с автором результат.
Ваше рассуждение содержит ошибку. Когда мы вычисляем условную вероятность события A при условии B (P(A|B)), мы должны умножить вероятность B на условную вероятность A при условии B, а не на условную вероятность A при отрицании B (P(A|!B)). Ваше выражение P(A) = P(A|B)*P(B)+P(A|!B)*P(!B) не соответствует этому принципу. Очень просто изложить рассуждение автора. Мы рассматриваем все возможные исходы, где второй игрок находится в сетке. Эти исходы равновероятны, так как мы считаем симметричную сетку. Затем мы умножаем это на вероятность того, что оба игрока выиграют свои матчи и встретятся в первом туре.