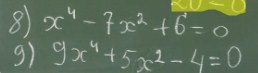Для получения решения уравнения с использованием формулы дискриминанта нужно выполнить следующие шаги:
1. Перепишите уравнение в общем виде: ax^2 + bx + c = 0, где a, b и c - коэффициенты.
2. Вычислите дискриминант D по формуле D = b^2 - 4ac.
3. Определите тип решений, исходя из значения дискриминанта:
- Если D > 0, то уравнение имеет два различных вещественных корня.
- Если D = 0, то уравнение имеет единственный вещественный корень.
- Если D < 0, то уравнение имеет два комплексных корня.
4. Используя формулу корней уравнения, найдите значения x:
- Если D > 0, то x1 = (-b + √D) / (2a) и x2 = (-b - √D) / (2a).
- Если D = 0, то x = -b / (2a).
- Если D < 0, то x1 = (-b + i√|D|) / (2a) и x2 = (-b - i√|D|) / (2a), где i - мнимая единица.
Относительно онлайн-калькуляторов для решения алгебраических задач, вот несколько надежных ресурсов:
1. Wolfram Alpha (https://www.wolframalpha.com/)
2. Symbolab (https://www.symbolab.com/)
3. Mathway (https://www.mathway.com/)
На этих ресурсах вы можете вводить свои уравнения и получать подробные ответы и пошаговые решения.