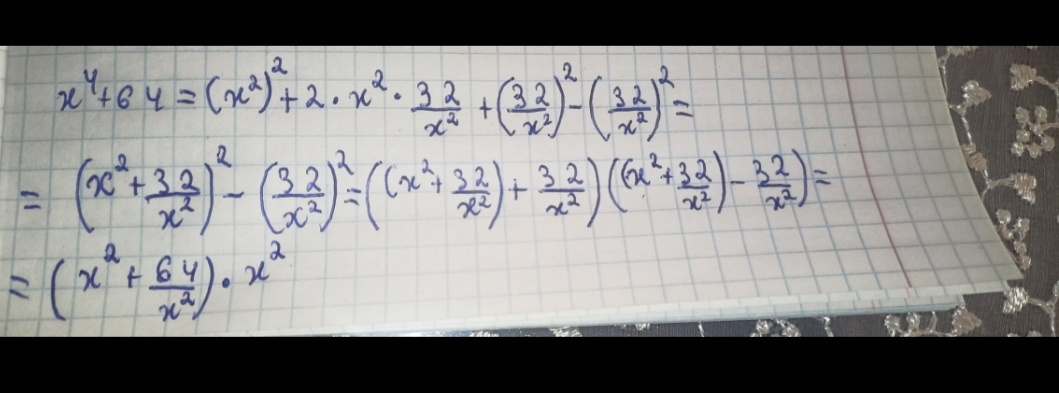Чтобы разобраться с решением данной задачи, следуйте указанным шагам:
1. Вначале примените выделение полного квадрата к данному многочлену. Для этого выразите x^4+64 в виде квадрата суммы двух членов.
Результат будет иметь вид:
x^4+64 = (x^2)^2 + 8^2
2. Теперь примените формулу разности квадратов к полученному выражению.
Разность квадратов выглядит следующим образом:
a^2 - b^2 = (a + b)(a - b)
Применив формулу к полученному многочлену, мы получим:
x^4+64 = (x^2 + 8)(x^2 - 8)
Таким образом, разложение многочлена x^4+64 на множители в результате применения выделения полного квадрата и формулы разности квадратов будет следующим:
x^4+64 = (x^2 + 8)(x^2 - 8).
Теперь вы можете сравнить данное объяснение с решением из учебника и убедиться в его правильности. Если у вас возникнут дополнительные вопросы или затруднения, не стесняйтесь задавать их.